pdf版题目

二阶魔方还原

by Siqi Na
时间限制: 1000 ms 内存限制: 10240 KB

问题描述

二阶魔方是 2x2x2 的立方体结构魔方，它共有 8 块，如下图所示：

我们可以定义魔方作为一个正六面体的六个面为 F(ront), B(ack), U(p), D(own), L(eft), R(ight)。我们根据先前后后，先上后下，先左后右的方法，依次给魔方的每一个方块编号，块编号的方式如下表所示：

带块编号的魔方平面展开图如下图所示：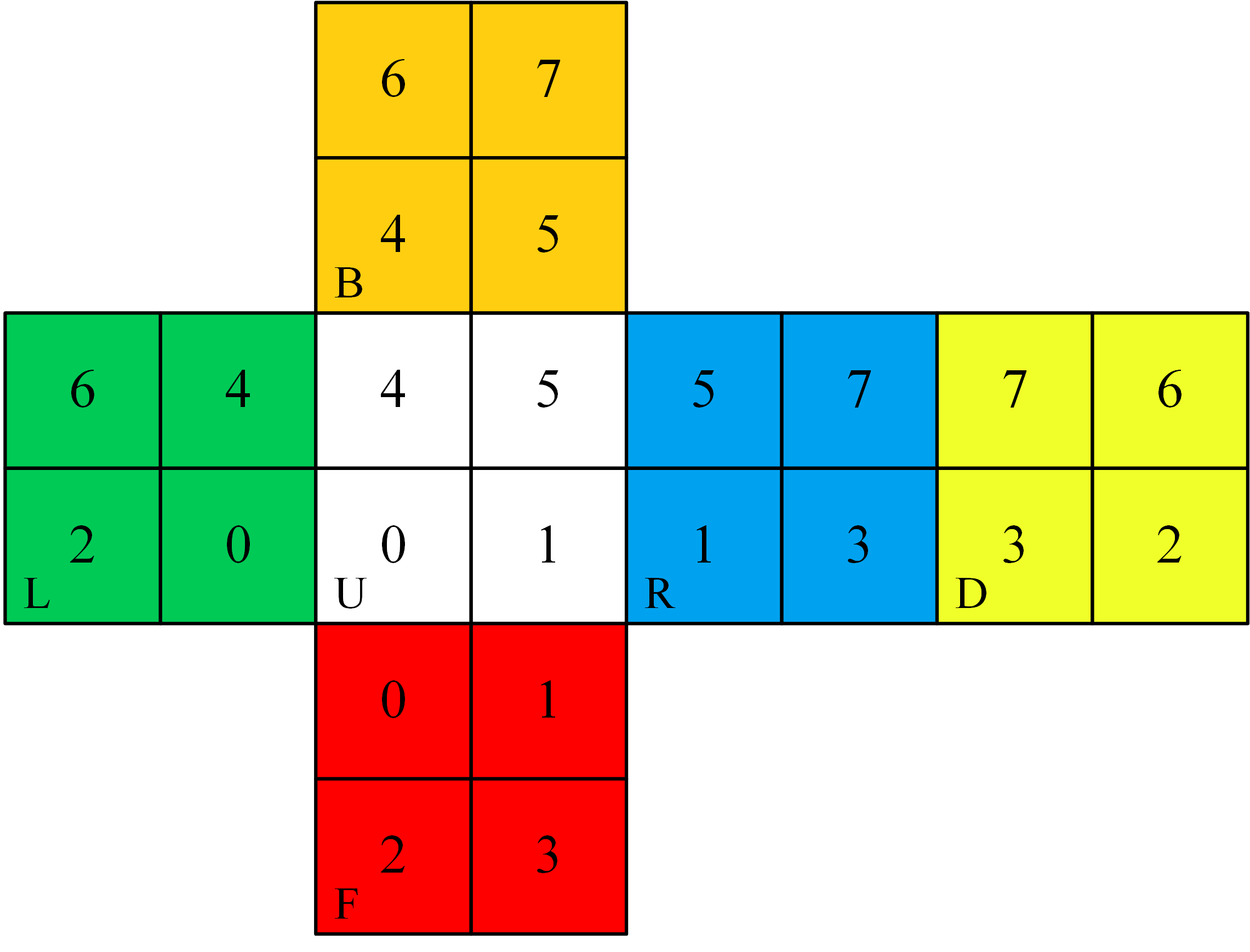

与三阶魔方不同，二阶魔方的每个块均有 3 个面露在外面，并被涂为不同的颜色，共 6 种颜色。我们定义整个魔方作为魔方共有 24 个面。任意两个面，如果颜色不同，那么显然是不同的两个面；若颜色相同，但与其在同一个块上的另外两种颜色不可能全相同，那么这两个面也是不同的两个面。因此，二阶魔方的 24 个面各不相同。所以我们可以给每个面一个编号（ 0 到 23 ），面编号的方式如下表所示（其中“ 0F ”表示“第 0 块；前面”）：

带面编号的魔方平面展开图如下图所示：

根据这种面编号的方法，一个复原后的魔方可以写成一个长度为24的数组： [0, 1, 2, 3, …, 23] ，一个被打乱的魔方可以写成这个数组的重排，例如下面的这种情况：

此时用数组表示这个状态为： [10, 11, 9, 5, 3, 4, 6, 7, 8, 22, 23, 21, 1, 2, 0, 14, 12, 13, 18, 19, 20, 17, 15, 16] 。

我们定义魔方的状态是不受视角影响的，也就是说只有拧动魔方后，其状态才会改变。这里我们可以分析一下二阶魔方存在多少种不同的状态。由于视角的不同，二阶魔方的每一种状态会对应到 24 种不同的如图 2 所示的平面展开图（6 个面均可作为正面，同时又可以以正面为轴滚动 4 次，得到 6x4=24 种不同的平面展开图）。二阶魔方 8 个块的位置均可任意互换（8! 种情况）。如果固定一个块作为参考，那么另外 7 个块中每个都可以有 3 种不同的朝向（37 种情况）。于是我们得到了 8!37 种不同的平面展开图。所以二阶魔方的状态总数为：

在还原二阶魔方的过程中，“FRU注释”是一种比较通用的还原步骤注释。FRU注释只旋转魔方的 正面（F: front）、右面（R: right）和 上面（U: up），并且可以分别 顺时针旋转90°（用+表示）、180°（用2表示）和 逆时针旋转90°（用-表示）。这样魔方每步就有 9 种的变化方式（注意到在可以调整视角的情况下其他的旋转方式是等价于这 9 种方式中的某一种的）。下图描述了FRU注释的操作过程：

若采用FRU注释的 9 种方式旋转魔方，对于二阶魔方的任意一种状态，最坏情况下只需要 11 步就可以将魔方还原。其中，在 3674160 种不同的魔方状态中，有一半左右（1887748 种）的状态最少需要 9 步才能还原魔方。下表给出了最少旋转次数和对应的状态总数的关系：

我们的问题就是：给出一个被打乱的二阶魔方（根据前文的方法表示成打乱顺序的数组 [0, 1, 2, 3, …, 23] ），求出还原魔方的最少步数（每步只能是FRU注释的 9 种操作的一种），并且按照 FRU注释 给出每步的具体操作以及每步操作后的结果（长度为 24 的数组）。

输入格式

输入为某种被打乱的魔方的状态，输入的格式为打乱顺序的数组 [0, 1, 2, 3, …, 23] 。

注意到FRU注释的9种旋转方式均不会改变魔方中一块的状态（后下左），所以还原后的魔方的状态由这个块的初始状态唯一确定。本题中为了使得还原后的魔方状态用数组表示为 [0, 1, 2, 3, …, 23] ，会保证所有测试数据的数组的 18, 19, 20 均在原本的位置。

输出格式

首先第一行输出一个正整数 n ，表示还原魔方所需的 最少 步数。

接下来的输出有 2n 行（若 n = 0 则无需输出）。第 (2i – 1) 行输出一个字符串，表示还原魔方的每步操作，字符串要求是 9 种旋转操作（F+，F2，F-，R+，R2，R-，U+，U2，U-）中的一种。第 (2i) 行输出一个长度为 24 的数组，这个数组表示经过第 (2i – 1) 行的操作后魔方的状态。

注意：使用最少步数还原魔方可以有多种操作方式，请输出任意一种即可。前 4 组测试数据保证最少步数不超过 7 步，后 6 组的测试数据无限制。

输入样例

10 11 9 5 3 4 6 7 8 22 23 21 1 2 0 14 12 13 18 19 20 17 15 16

输出样例

2
U-
0 1 2 11 9 10 6 7 8 22 23 21 12 13 14 4 5 3 18 19 20 17 15 16
R-
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

提示

本题可能需要了解“状态空间搜索”、“状态压缩”和“双向广度优先搜索”。这部分内容可以参考百度百科的 搜索算法。

1 状态空间搜索

状态空间搜索就是将问题的求解过程转化为从初始状态到目标状态寻找路径的过程。状态空间可以看成一个图，图上的点就是某个 状态 ，边则是某个状态到另一个状态的 状态转移 关系。使用状态空间搜索求解问题的关键就是：利用有效的数据结构对状态进行存储，实现状态间的转移关系，进而使用 深度优先搜索 或 广度优先搜索 算法计算初始状态到目标状态路径。

本题中，状态就是魔方的状态，即长度为 24 的数组，状态转移关系则是FRU注释中的 9 种操作。

所以，我们需要把FRU注释中的 9 中操作对应的颜色变换列举出来（即变换后的面的编号对应原来的哪个编号），然后依据输入给的初始状态，通过广度优先搜索遍历可能转移到的状态，直到搜索到最终状态( [0, 1, 2, 3, …, 23] )，便求出了还原魔方的最少步数，并且可以通过回溯得到每步的操作。

2 状态压缩

在搜索的过程中，我们需要标记哪些状态已经被访问过了。对于简单的搜索，我们可以直接用 bool 数组来标记状态访问与否。但是，本题的状态是一个长度为 24 的数组，我们需要建立哈希表来存储。为了简化程序，这里建议大家直接使用 C++ STL 中的 map 或 unordered_map 来实现哈希表，并且状态的表示也用 STL 中的 vector 而不是数组（因为 vector 可以直接用在 map 中，而数组不行）。不过，用数组或 vector 表示一个状态会占用较多的内存，并且会延长哈希表定位键值的时间。
状态压缩要考虑的问题是如何用 更有效的方式对状态进行编码。对本题而言，注意到只有 6 种颜色，所以可以先将颜色编号( 0 ~ 5 )，进而使用 六进制 对长度为 24 的状态数组编码：六进制的第 i 位，表示第 i 个位置的颜色。所以我们需要一个取值范围在 0 ~ 624-1 的数字来表示一个状态，这个取值范围恰好在无符号 8 字节整数（C++中的 unsigned long long）的取值范围（0 ~ 264-1）内。于是，我们在使用 map 标记状态时，就不需要使用 vector 作为键值，而是使用这个 unsigned long long 的编码值了。比如最初状态的数组使用六进制状态压缩的表示为：

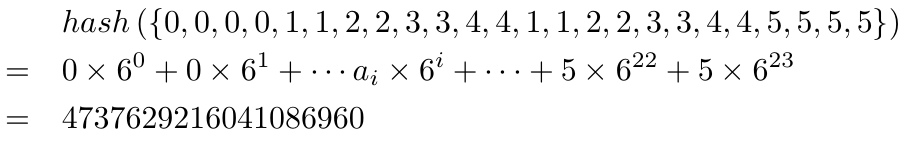
而我们要获取第 i 个位置的颜色时，便可直接让压缩后的编码对 6i+1 取模后，再对 6i 取整即可。
也可以根据块编号以及块状态进行编码，8 块的其中一块（块编号为6的块）的位置及状态已经是确定的了，因此最多只有 7 个块的顺序( 7! )及7个块的状态( 3^7 )。实际上确定了剩余 7 个块中 6 个块的状态，最后一个块的状态就已经确定了，因此总状态数为( 7!*3^6 = 3674160 )，与前面的分析相同。所以可以使用14位的 unsigned long long 进行编码，如还原后的状态为：01234570000000（前 7 位表示块的位置，后 7 位表示每个块的状态( 0, 1, 2 )）。
当然，以上两种压缩方法只是简单的例子，存在更好的压缩方式，因为总状态数仅有 3674160 种。

3 双向广度优先搜索

广度优先搜索的过程中需要维护一个存储待搜索状态的队列，因此广度优先搜索的问题就是会占用很大的内存。而对于目标状态确定的问题来说，双向广度优先搜索是减少内存开销的一个有效手段。双向广度优先搜索的思想就是 从 初始状态 和 目标状态 同时进行广度优先搜索，保持搜索的层数同步，最终两个方向的搜索所遍历的状态会在中间相遇，从而求出了最短的路径。这样一来便减去了很多不必要的搜索状态，因为搜索的过程中每层的状态数是近似成倍增加的。

使用双向广度优先搜索需要确定初始状态和目标状态。对于本题而言，初始状态是直接输入的，而目标状态即为 [0, 1, 2, 3, …, 23]。另外，对于本题而言，若前一步的操作为F(+, -, 2)，则后一步的操作不会仍为F(+, -, 2)，因为任意连续的两次以上F的操作可以用某种一次以下F的操作表示，U和R同理。依此编写代码也可以减少时间和空间的开销。

PS：建议尽可能精简代码，重复的代码封装成函数调用，充分利用数组，以减少出错的可能性。

我的代码

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;

string ro_name[9] = {
    "F+", "F2", "F-",
    "R+", "R2", "R-",
    "U+", "U2", "U-"
};

int rotation[9][24] = {
    {6, 7, 8, 0, 1, 2, 9, 10, 11, 3, 4, 5, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23},
    {9, 10, 11, 6, 7, 8, 3, 4, 5, 0, 1, 2, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23},
    {3, 4, 5, 9, 10, 11, 0, 1, 2, 6, 7, 8, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23},

    {0, 1, 2, 11, 9, 10, 6, 7, 8, 22, 23, 21, 12, 13, 14, 4, 5, 3, 18, 19, 20, 17, 15, 16},
    {0, 1, 2, 21, 22, 23, 6, 7, 8, 15, 16, 17, 12, 13, 14, 9, 10, 11, 18, 19, 20, 3, 4, 5},
    {0, 1, 2, 17, 15, 16, 6, 7, 8, 4, 5, 3, 12, 13, 14, 22, 23, 21, 18, 19, 20, 11, 9, 10},

    {5, 3, 4, 16, 17, 15, 6, 7, 8, 9, 10, 11, 1, 2, 0, 14, 12, 13, 18, 19, 20, 21, 22, 23},
    {15, 16, 17, 12, 13, 14, 6, 7, 8, 9, 10, 11, 3, 4, 5, 0, 1, 2, 18, 19, 20, 21, 22, 23},
    {14, 12, 13, 1, 2, 0, 6, 7, 8, 9, 10, 11, 16, 17, 15, 5, 3, 4, 18, 19, 20, 21, 22, 23}
};

vector<int> ro(vector<int> v, int x) {
    vector<int> data(24);
    for (int i = 0; i < 24; ++i) {
        data[i] = v[rotation[x][i]];
    }
    return data;
}

int ro_reverse(int i) {
    switch (i) {
        case 0:
        case 3:
        case 6:
            return i + 2;
        case 2:
        case 5:
        case 8:
            return i - 2;
        default:
            return i;
    }
}

vector<int> pos2color(vector<int> arr) {

    int colors[6][4] = {
        {0,  3,  6,  9 },
        {1,  8,  14, 19},
        {2,  4,  13, 17},
        {5,  10, 16, 23},
        {7,  11, 20, 22},
        {12, 15, 18, 21}
    };

    for (int i = 0; i < 24; ++i) {
        for (int j = 0; j < 6; ++j) {
            for (int k = 0; k < 4; ++k) {
                if (arr[i] == colors[j][k]) {
                    arr[i] = j;
                }
            }
        }
    }
    return arr;
}

void print(vector<int> arr) {
    if (!arr.size()) {
        cout << endl;
        return;
    }
    cout << arr[0];
    for (int i = 1; i < arr.size(); ++i) {
        cout << " " << arr[i];
    }
    cout << endl;
}

ull color2num(vector<int> arr) {
    ull p[24] = {1, 6, 36, 216, 1296, 7776, 46656, 279936, 1679616, 10077696, 60466176, 362797056, 2176782336, 13060694016, 78364164096, 470184984576, 2821109907456, 16926659444736, 101559956668416, 609359740010496, 3656158440062976, 21936950640377856, 131621703842267136, 789730223053602816};
    ull n = 0;
    for (int i = 0; i < 24; ++i) {
        n += arr[i] * p[i];
    }
    return n;
}

vector<int> num2color(ull n) {
    vector<int> v;
    while (n) {
        v.push_back(n % 6);
        n /= 6;
    }

    return v;
}

void bfs(vector<int> arr) {
    map<ull, vector<int>> step[2];
    queue<ull> q[2];

    ull init = 3021148815593781390;
    q[0].push(init);
    step[0][init] = vector<int>();

    auto c = pos2color(arr);
    ull n = color2num(c);
    q[1].push(n);
    step[1][n] = vector<int>();

    if (n == init) {
        cout << 0 << endl;
        return;
    }

    /* print(m[n]); */

    for (int x = 0; ; x = !x) {
        int q_size = q[x].size();
        /* cout << "size  " << q_size << endl; */
        for (int i = 0; i < q_size; ++i) {
            ull k = q[x].front(); q[x].pop();
            for (int i = 0; i < 9; ++i) {
                /* auto v = ro(m.at(k), i); */
                auto v = ro(num2color(k), i);
                v.reserve(24);
                ull n = color2num(v);
                /* print(v); */

                if (step[x].find(n) != step[x].end()) {
                    /* cout << endl; */
                    continue;
                }

                vector<int> s(step[x].at(k));
                s.push_back(i);
                /* print(s); */

                if (step[!x].find(n) != step[!x].end()) {
                    /* cout << "find" << endl; */

                    vector<int> &a = s, &b = step[!x].at(n);

                    if (!x) {
                        swap(a, b);
                    }

                    vector<int> ans(a);
                    for (auto p = b.rbegin(); p != b.rend(); ++p) {
                        ans.push_back(ro_reverse(*p));
                    }

                    cout << ans.size() << endl;

                    vector<int> v(arr);
                    for (int i : ans) {
                        cout << ro_name[i] << endl;

                        v = ro(v, i);
                        print(v);
                    }

                    return;
                }

                step[x][n] = s;
                q[x].push(n);
            }
        }


    }




}

int main() {
    vector<int> v(24);
    for (int i = 0; i < 24; ++i) {
        cin >> v[i];
    }

    /* iota(v.begin(), v.end(), 0); */
    /* srand(time(nullptr)); */
    /* for (int i = 0; i < 10000; ++i) { */
    /*     v = ro(v, rand() % 9); */
    /* } */


    bfs(v);




    return 0;
}

一些草稿